Fish don’t know they’re in water. If you tried to explain it, they’d say, “Water? What’s water?” They’re so surrounded by it that it’s impossible to see. They can’t see it until they jump outside of it.

Derek Sivers

Sitting in a park in central London on a warm, sunny June 2018 day I knew something in me had shifted forever. My head was full of swirling mathematical thoughts processing just what had happened during those last hours. Before this day, I had no interest in working with multi-base. It seemed impractical and if I am honest, an unnecessary indulgence. But something in my brain was broken and unresolved after I was unable to do an exercise at that CPD workshop. And I had to get to the bottom of it. So I began a journey of curiosity, frustration and wonder into the world of multi-base.

That CPD day was delivered by La Salle Education CEO Mark McCourt and was titled “Making Maths Memorable”. I had learnt many things that day, including the split attention effect, non-examples and the careful use of silence when presenting visual information. The workshop wasn’t a multi-base workshop as such but it had clearly piqued my interest. Over the years I started adapting ideas from the workshop to my seemingly alien world of online tutoring. My teaching was to be transformed.

It took me several months to do anything with multi-base after that workshop, perhaps because I had no starting point or representation to grip the idea. Until I heard about numbers, numerals and digits in a podcast by Mark again. It turned out I didn’t know abut this either. How could I convey these early, basic ideas to my tutees if I didn’t understand them myself? There was a big, gaping blind spot in my teaching staring back right at me. It existed because none of these things are tested in the current English maths curriculum or any of the other systems I had encountered. And I’ve tutored in over 25 countries! So if it isn’t tested for in any curriculum then is it worth learning?

Well obviously yes, because mathematicians are curious and seek enlightenment. I knew that understanding number in depth held an important key, not just for my lowest attaining pupils, who I felt would benefit most from the knowledge at first, but for all pupils. I looked up various definitions and started exploring the world of numbers. Having grown up in Libya and India I was already familiar with modern Eastern Arabic numerals and Hindi Devanagari numerals.

If you want to master something, teach it. A great way to learn is to teach.

Richard Feynman

I found a Year 7 tutee to test my ideas and understanding with multi-base. I had tutored her since Year 5 and her parents were open minded on my teaching of ideas beyond the curriculum. She was a diligent, curios and bubbly learner. She was honest and clear live when teaching : “I don’t get this”, “What do you mean when you say numeral?” etc., This batting to and fro was what I needed to tweak and refine my delivery in real-time. This is a fairly routine aspect of tutoring, a conversation and constant running of experiments to gauge where the tutee is at.

With my help she made an odometer type counter on our digital writing platform Bitpaper by programming the numerals in steps of 1. Pressing the forward or rewind button (Undo and Redo) would get the odometer to count up or down in various bases. Much like the counter of fuel at a petrol station does in base-ten. An odometer counting up is all I could think of and I didn’t come back to multi-base again for a few more months. Unknown to me there was a bigger issue I had to resolve first.

An immediate problem I faced was that the number system in base-ten was so deeply ingrained in my mental programming that it was difficult to think outside of it. Whenever I saw 14 written in various bases, I read and saw it as fourteen. I needed numerals from another language altogether to break the association of base-ten with the way digits are combined to make everyday numerals. I found the perfect bridge both for me and tutee by using Hindi (or Devanagari) numerals.

It is somewhat embarrassing to admit that despite having grown up in Libya, Yemen and India, I had no idea that the modern numerals we use today are Hindu-Arabic numerals. It is never too late to learn of course and it sure makes for good stories with tutees. Incidentally, Libya has a lot of Roman monuments preserved immaculately, so I was surrounded by a blend of ancient Roman numerals, Hindi numerals and Eastern Arabic numerals during my childhood days in Tripoli. It felt amazing to look back at something so familiar and find deeper meaning through these numerals.

Over the next two years I attended various other La Salle CPD days in London on multiple representations. Each one had a mention of numbers, digits and numerals and counting in different bases. I read books, found videos and podcasts too. I started to see how the area model could be used to understand number systems in other bases. In particular the use of Dienes blocks which Zoltan Dienes used in various other bases. I even got hold of an incomplete set of physical wooden sets of multi-base blocks, which looked very cool. My understanding was starting to deepen, but I didn’t feel confident enough to start teaching with virtual multi-base blocks, the only ones I could use online with my tutees. Base-ten blocks were no problem at all and I was using them before anywyay.

In all this time, I started to fine tune my skills in teaching through various representations. Particularly the use of the Rekenrek, algebra tiles, Cuisenaire rods and two sided counters. After seeing a back to back session on the use of two sided counters by Jonathan Hall (aka mathsbot) and Bernie Westacott, I started to realise how incredibly effective two sided counters could be for teaching so many mathematical ideas.

Fast forward to March 2020; a global pandemic happened and life turned upside down. I was fortunate that I kept tutoring online as I had done for all these years and that time was well spent in exploring virtual manipulatives to teach students in far flung corners of the globe. This experience of operating in the virtual 2-D world of online tutoring was about to pay dividends in how I could understand and teach multi-base. Not just to my tutees but as CPD later, both receiving and delivering it.

#MathsConf23, like many events, went virtual a few weeks into pandemic. The “Explode your mind with exploding dots: A global phenomenon” presentation was given by James Tanton who radiated a teaching life force and infectious enthusiasm. By then I had already been using dots/counters/rekenreks, so I got this representation immediately. For the first time, multi-base started to make clear sense and a whole new universe revealed itself to me. I was breaking out of the shackles of base-ten.

I then started helping my tutees prize this association apart. Disrupting someone’s worldview is no easy task but my tutees trust me. Besides, younger tutees had not lived with base-ten for as long as I had, so they were fairly quick to grip multi-base. Nonetheless, I took an incredible amount of care and caution to make sure that tutees do not get muddled up. Always starting from an open ended exploration of numbers, digits and numerals before presenting clear cut definitions. Regularly reminding them that a numeral is the written code and representation of number, whereas number is the thing itself, the idea.

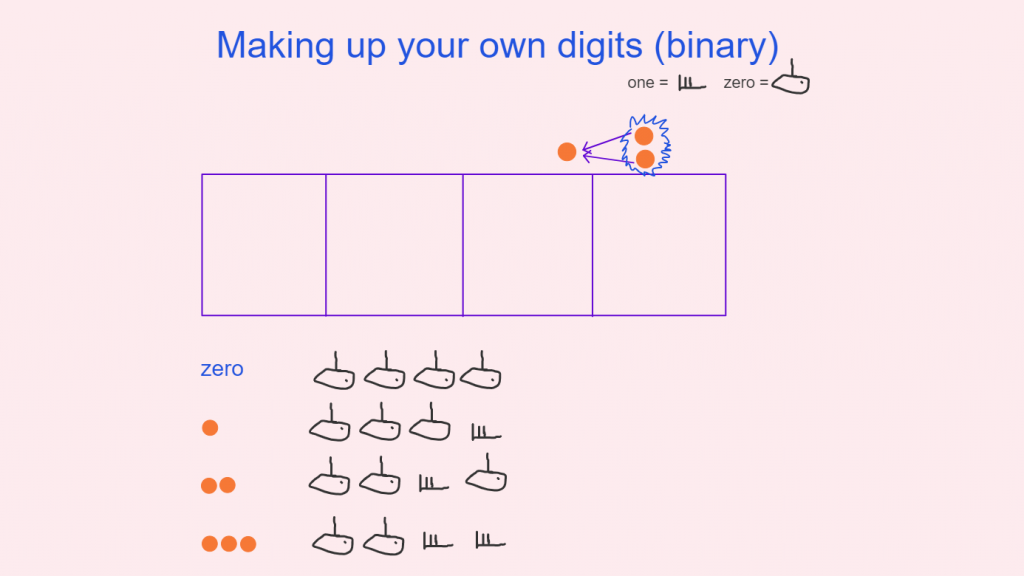
I sidestepped working in multi-base with Hindu-Arabic numerals with my tutees and started using a mix of ancient Egyptian and Roman numerals first. Roman numerals turned out to be a great bridge into this world for my tutees as they were already familiar with them. And in this last academic year, I have thoroughly explored exploding dots as my go to representation for multi-base, both with whole numbers and whole + fractional numbers.

I have now emerged on to the other side; now when I see 14, I see a numeral that is one-four. A symbol that could represent various other numbers depending on base choice. I even get the joke: “There are 10 types of people in this world, those who understand binary and those who don’t”! And since September 2020 I have been covering a range of multi-base ideas with tutees, from long addition algorithms to division. It is only a few months on but I am already seeing them develop robust and flexible generalising skills. They are becoming more mathematical and some of them are already comfortable working in base-x.

I have a lot more to write about teaching multi-base and will do so in a series of blog posts, particularly on the idea of place value. Once you are enlightened about place value, it is impossible to teach place value in just base-ten. Because teaching it in just base-ten does not feel like teaching place value at all. Education and CPD is the way out of this, just like it has been for me. Place value in other bases has also been mentioned by Charlotte on her blog post and there are some really great definitions of various related ideas on Mark’s blog post too.

So how to get started on multi-base (radix)? You can of course look it up online, in various books or take CPD. The exploding dots website is a great place to get started on it. I presented a workshop at #MathsConf25 titled “An introduction to Multi-base” which was specifically designed for complete novices with my fresh viewpoint. I really encourage maths teachers, tutors and pupils to explore the world of multi-base. There is something profound missing if you don’t understand it.

Disrupting one’s own existing worldview and frame of reference is no easy process. But as teachers we know this better than anyone else. An incredible journey awaits for you if you haven’t explored this world yet and want to dive into it.